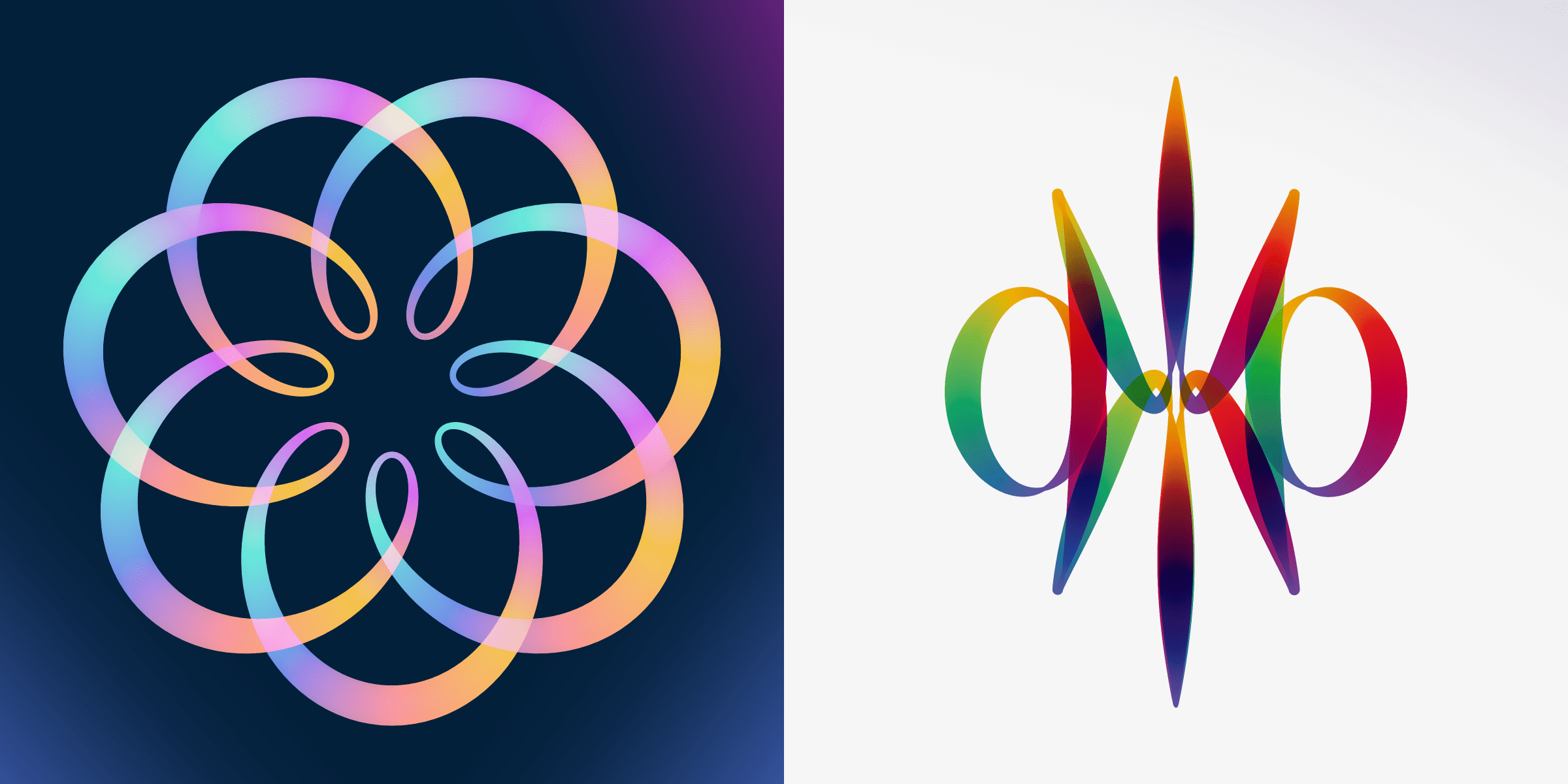“Rotae” is a generative art collection that I created for Art Blocks. It is based on, and is an ode to, the vast array of beautiful shapes that can appear from the seemingly simple process of letting circles rotate on (many more) circles. The name of the project, Rotae, means “wheels” in Latin, and is a nod to the paper that describes the math behind finding a certain m-fold symmetry, regardless of the number of circles that are chained together.

“Rotae” is now fully minted! You can see the gallery with all 529 outputs here and if you’re interested in getting a Rotae from the secondary market, you can find the collection on OpenSea. If you already own a Rotae, check out the Animating the Wheels section below where you can input the hash of your piece and see the underlying wheels that make up the shape!
Each shape is also animated after a few seconds, which can reveal the intricacies of the underlying path, and sometimes even reveal a most surprising hidden shape, such as a heart in the video below.
For more fun, you can play with Rotae on PopRank to decide which one you prefer between any two results, and thereby help determine the overall visual ranking of the collection! (It’s also quite addictive I have to admit (^∇^) )
The Technique
Using a hash as its seed, the pseudo-random-number-generator chooses the number of wheels (between 3 and 8) and what m-fold symmetry to create. Next, the wheels are randomly given radii and frequencies that will create the aimed-for symmetry.
Working from the symmetry towards the wheel settings (plus a few nudges here and there) makes sure that you don’t end up with paths that have to go around for tens or hundreds of times before finally closing again, which usually result only in very round shapes. Instead, using the symmetry math from the paper it’s possible to create shapes with a symmetries below 10-fold, giving a seemingly endless variety in what comes out, and clearly showing the path.
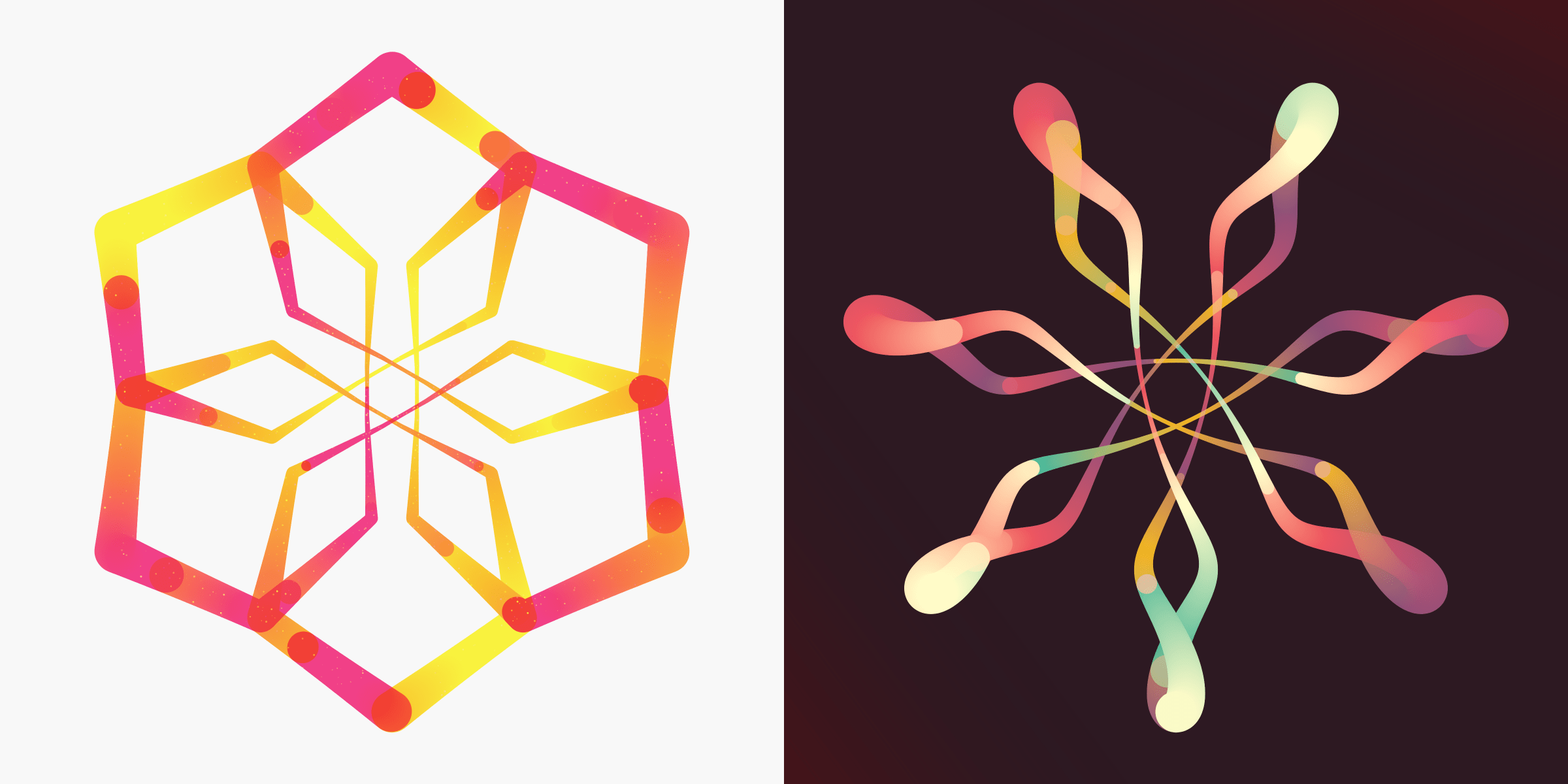
Animating the Wheels
I find that the shapes can take such unexpected forms that I’m sometimes almost doubting that it’s been drawn by simple circles systematically going around and around! I’ve therefore created the animating demo below. By default it takes a random hash, but you can also input the hash of any mint (specifically meant for the Rotae mints of course) and this will reveal how the final shape is drawn from its collection of circles/wheels, plus give you the detailed information about each wheel, such as its size and frequency.
The tokenData.hash that is used for the seed of the random number generator is not the same as the transaction hash that you see on the etherscan.io page of your transaction. Instead, you can find it by going to the mint’s page on Art Blocks, clicking the little “square with arrow pointing to the top-right” icon you can see in the lower right of the mint image. This will open up a new page with the mint itself. Next go to the devTools (generally you can right-click the page anywhere and choose “Inspect”). Within the devTools console type tokenData.hash and there is your hash! For example, try 0xd6eb1c4648814d31f830f69321bd7460b1d096a0db6e9b2a3ae709d4e836c679 which is the tokenData hash of mint #0 of Rotae. See the video below for a visual explanation on how to find the tokenData.hash.
Note | the animation will always show the “normal” smooth path for any hash, also for the mints that have their feature of path equal to angular. In those case the shape below can look a bit / quite different from how the minted version looks.
Input the TokenData Hash
Hash
...
Symmetry
...
To explain what the different columns mean:
- Wheel | The number of the wheel, starting from the wheel in the center. Wheel 1 is placed on the center, wheel 2 is attached to wheel 1, wheel 3 is attached to wheel 2, etc.
- Radius | The normalized radius of the wheel. All wheels together should add up to ±1. Not always though due to some rounding going on, especially when the number of wheels is large, but it should be pretty close.
- Frequency | The frequency of the wheel. In this case it shows how many full rotations (of 360°) the wheel will make before the path is complete. A positive number means the wheel is rotating counter-clockwise while a negative number indicates a clockwise rotating wheel.
- Usually this is the other way around. However I flipped the
Math.cosandMath.sinfor thexandyposition because I preferred the orientation of 2-fold symmetries to be upright ʕ•ᴥ•ʔ
- Usually this is the other way around. However I flipped the
With this you theoretically have all the info you’d need to recreate the base path of the shape yourself if you feel like it (⌐■_■) You can find more about the math of spirographs, and more generally “wheels rotating on wheels”, on this and this page.

Design
Let me explain all of the different features possible within Rotae that have nothing to do with the shape of the path, but instead with how it appears visually.
Drawing Style
There are several ways in which the path can be drawn. The most common is the default full line which is used for 68% of the pieces:
There is also an ellipse that rotates as the path is drawn, which becomes more magical as you watch the animation of the line. There is both a filled and stroked ellipse (only 9 pieces are in the stroked ellipse style, with 76 in the filled ellipse style, together about 16% are drawn in this ellipse style). Furthermore, if the path type of a stroked ellipse style is angular the shape becomes a diamond, which you can see for Rotae #237!

There is also a style that mimics the Italian calligraphy pen, with the straight oblique nibs. This results in the line creating wide paths when moving in certain directions and very thin ones for other directions. There are 38 Rotae with this style (7%).
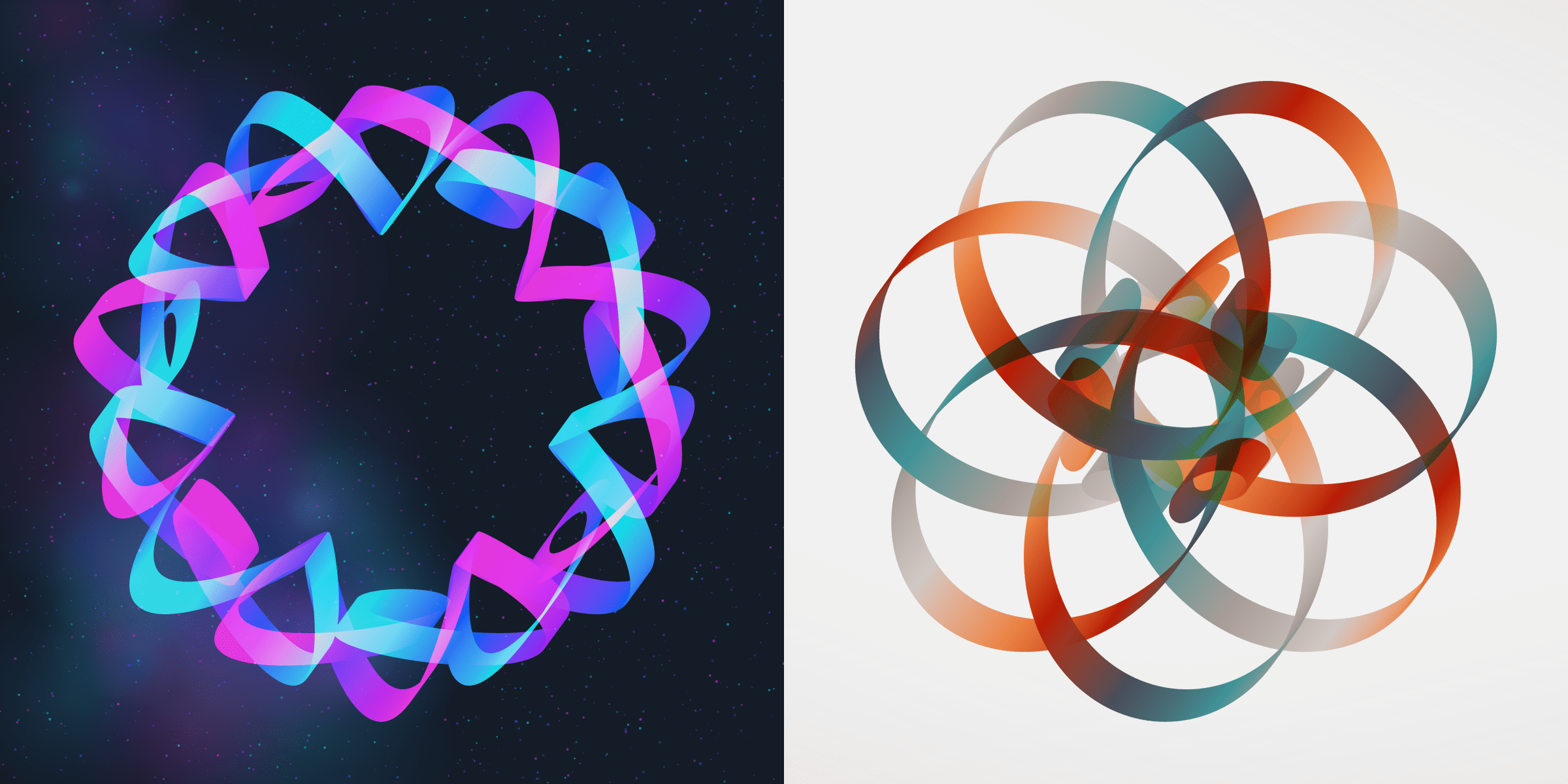
Another style uses lots of circles to fill in the space of a regular line, called confetti. There are 29 of these Rotae (5%).
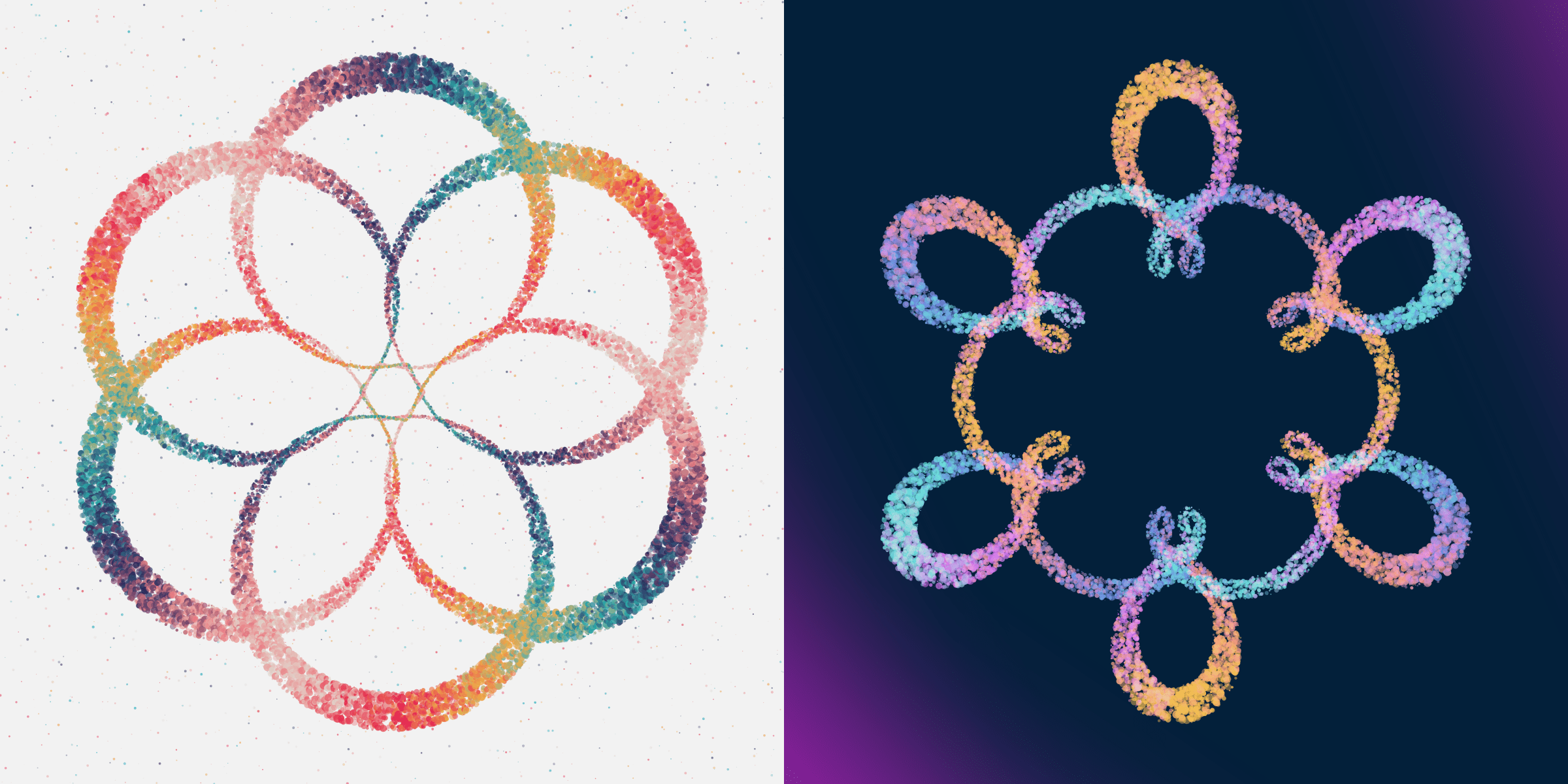
The two rarest styles draw the line with either clearly separated squares and circles. For the square style you can also have filled and stroked squares. There are only 2 Rotae with the filled style, giving an almost pixel-art feel, and 8 Rotae with the stroked squares.
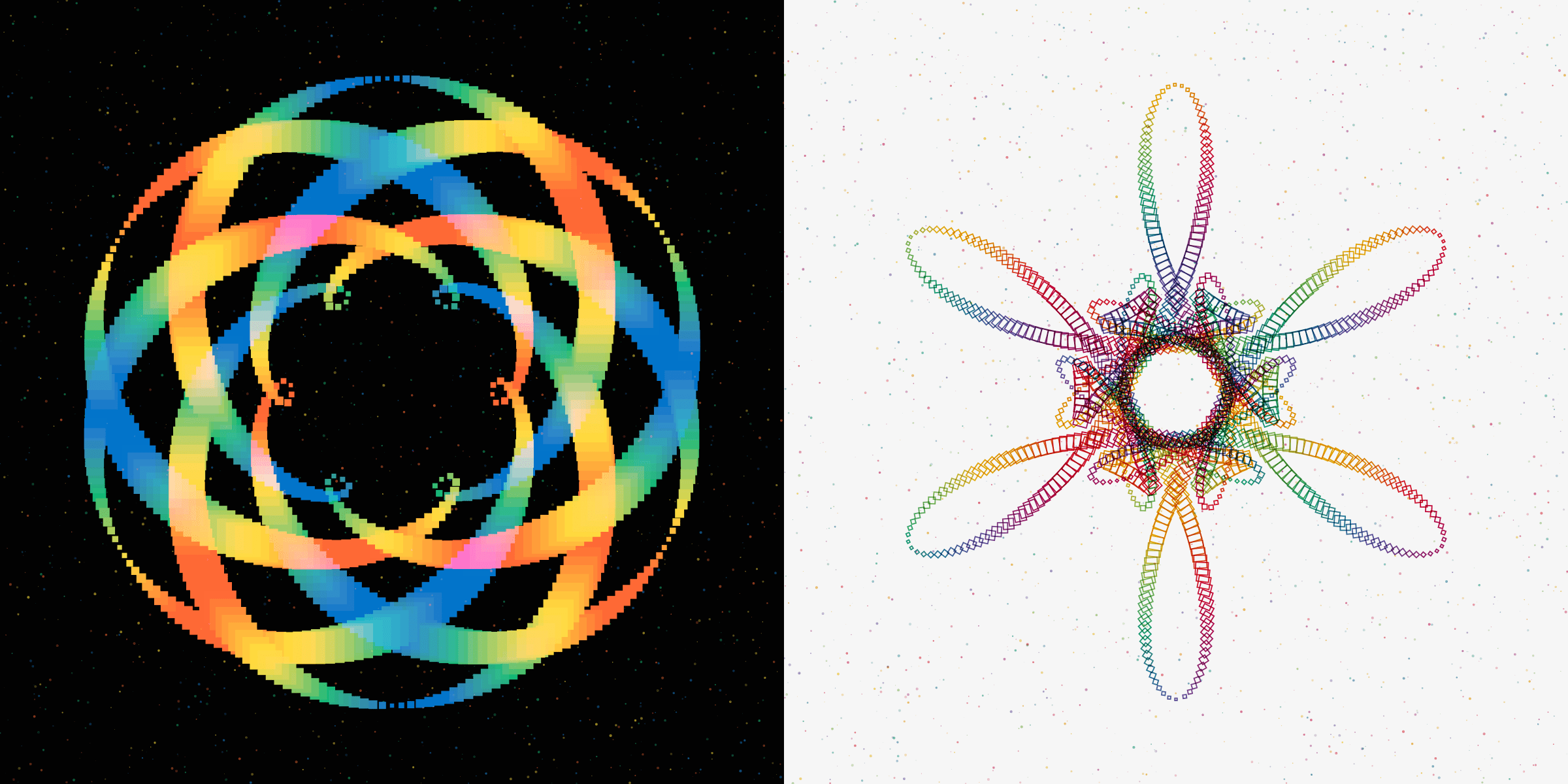
The circle style strings together circles along the path, increasing and decreasing in size. There are 7 of these Rotae.
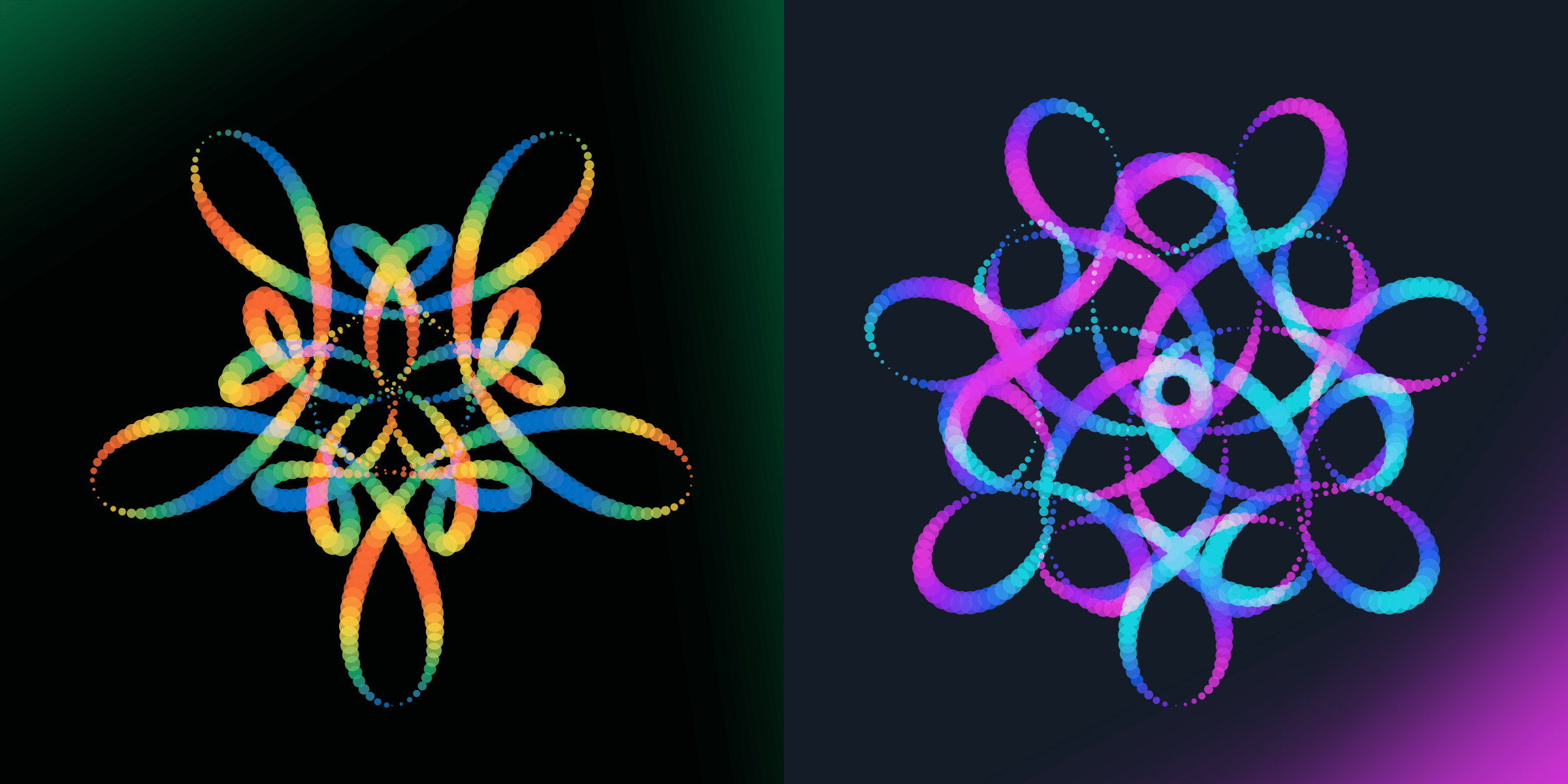
Radial Style
Even within the drawing style of using a fixed line, ellipse, or another shape there are different ways in which that line behaves. However, most of these radial styles appear within the line drawing style only, with most other drawing styles having either one or two of the options shown below.
There is the fixed line, which is a big chunky line that stays the same radius throughout. This is generally used for Rotae with relatively short paths (84, or 16%, Rotae have this feature).
There is also a distance radial style where the line gets thinner the closer it gets to the center, used for 152 Rotae (29%)

Another one mimics a thick brush style that gets thicker and thinner along the path, with 142 Rotae (27%). Like the fixed radial style this one also generally works best for the shorter paths.
For the (very) long paths there is a thin brush equivalent instead, with 139 Rotae (26%).

Finally, there is the thin style that is used specifically with the ‘Italic calligraphy’ nib drawing style for very long paths (with 11 Rotae (2%)).
Path Type
The final feature that has an impact on path itself is whether or not the line is draw in a smooth way, or if the path takes large jumps in between sampling from the mathematical formula, create interesting angular results (76 Rotae are drawn in an angular style (14%))

Color Palette
Rotae has 17 different color palettes. The palettes are spread out pretty evenly across all Rotae, ranging between 3% - 8% of the full collection. Many have very vibrant colors because of personal preferences (⌐■_■)
Space (9%) and Sunset (10%):

Fog (5%), which uses a randomly picked (dark) hue as the background, and Taxi Cab (3%):

Hot / Cold (6%) and Antique (6%):

Doogle (9%) and One Hue (3%), where the latter randomly chooses its (dark-ish) hue:

Viridis (5%), which is based on a good and popular data visualization color palette, and 80’s Pastel (6%):

Winter Fire (6%) and Popsicle (4%):
Dark Rainbow (8%) and Chaos (6%), with the latter being one of my favorite color palettes and one that I’ve used across all of my long-form NFT collections since, always named Chaos:
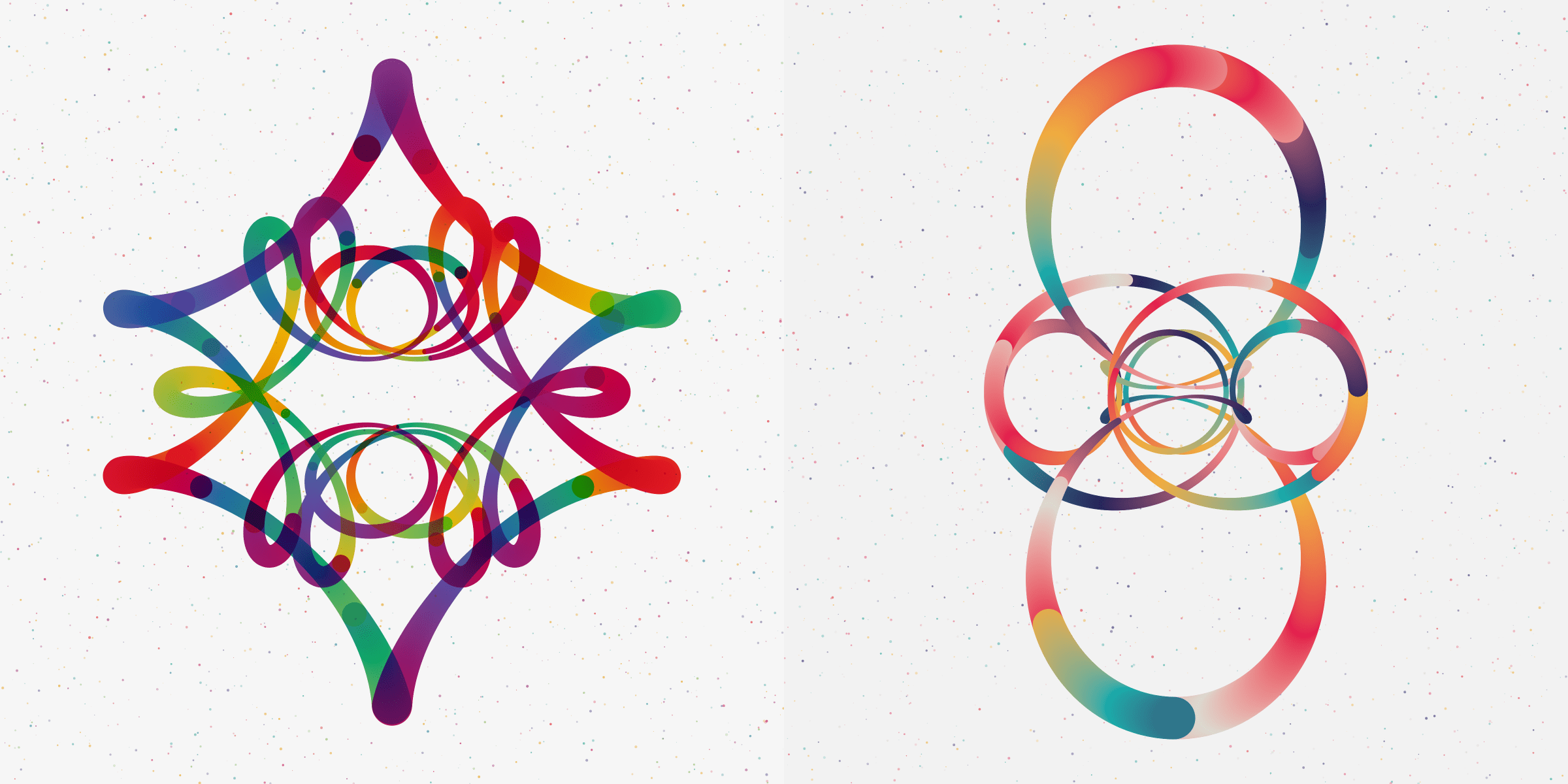
Maleficent (4%) and Queen of Hearts (5%). As a Disney fan I used inspiration from these two wonderful villainesses:

And finally there is the Snowflake (7%) color palette, which always has a dots background to give the illusion of some snow:

Color Flow
Each color palette is defined as a gradient between certain colors. The color flow feature determines if the line should be drawn from that continuous palette, or if the gradient should be discontinuous, broken along the line and started in a completely different section within the gradient again. The latter creates a feeling of colored “sections” within the line. There are 298 Rotae with the discontinuous setting (56%) so it’s pretty evenly split between the two.
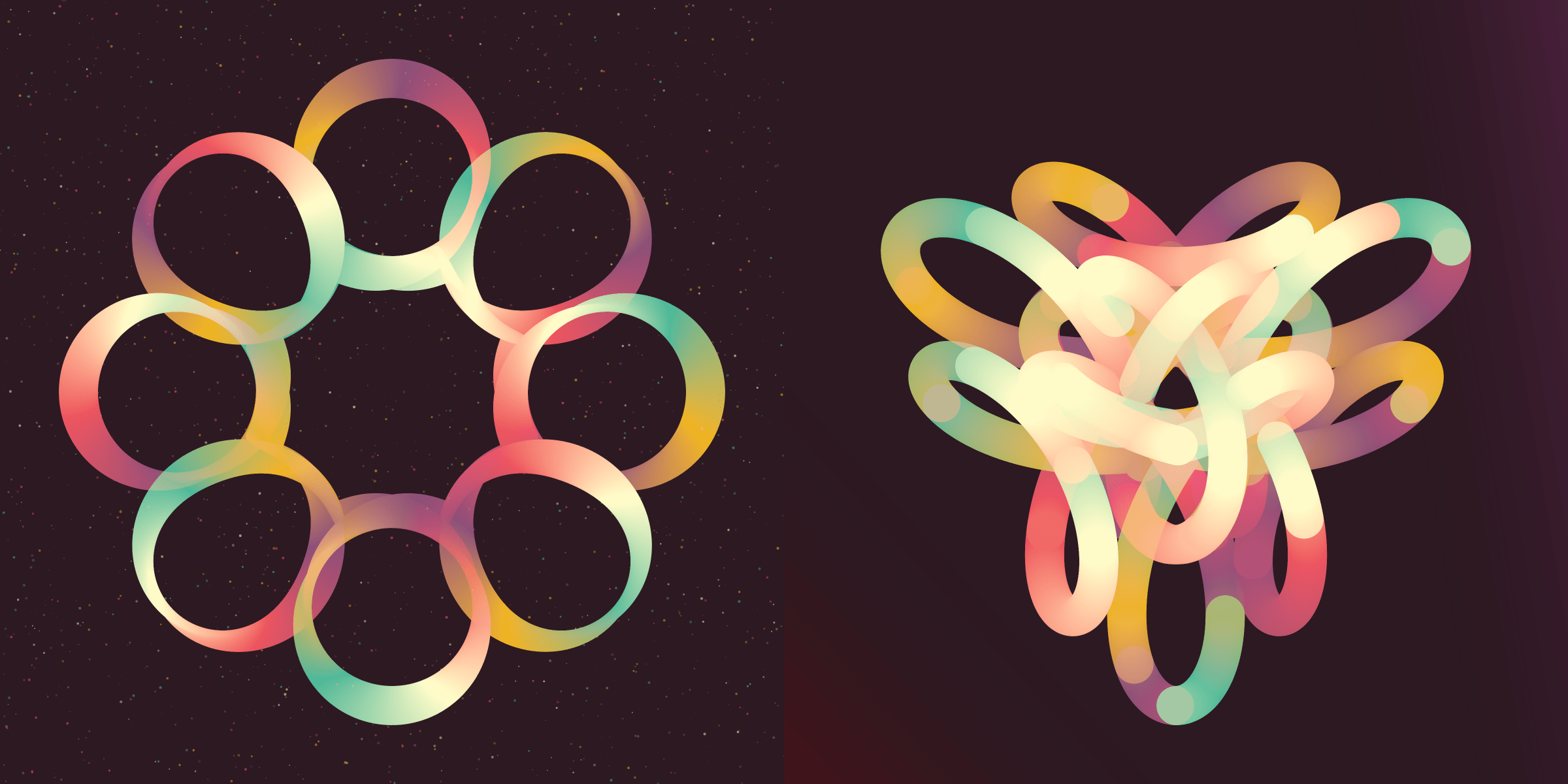
Background
There are four different background effects. From an even colored background (which is always the case for the taxi cab color palette), used for 59 Rotae (11%)

The most common background uses gradients. Some are very obvious, using colors quite different from the background, while others are so subtle that you have to really look before you’ll notice the soft fade between colors. There are 279 Rotae with the gradient background (53%).
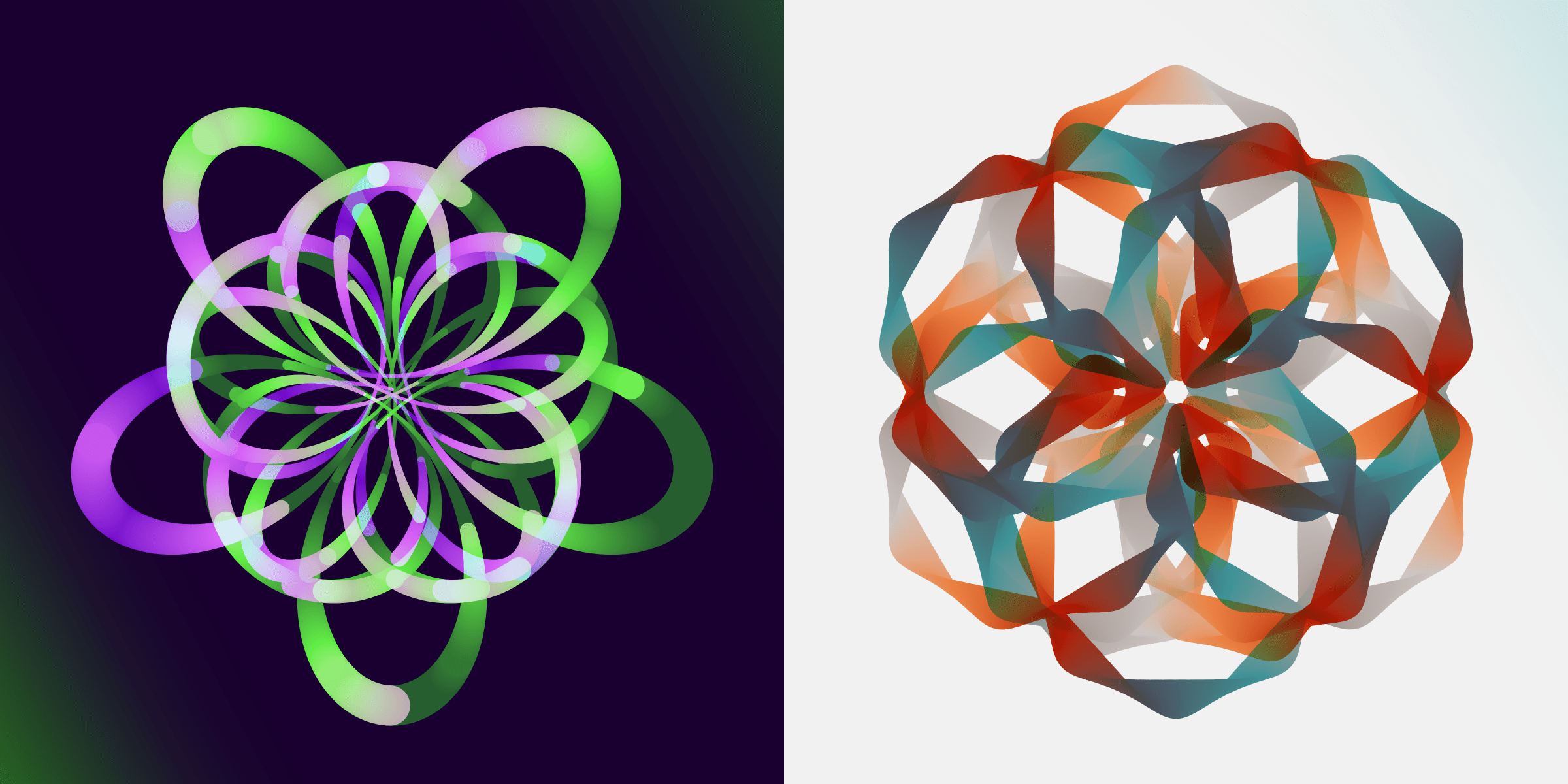
My personal favorite is probably the dots background that fills the background with hundreds of tiny dots, like splatters of paint. For the space color palette however, these turn into stars and vague nebulous areas are drawn to really get that space vibe. There are 160 Rotae with a dots background (30%).

Finally there is the pop background, which is the rarest with 30 Rotae having this feature (6%). This only happens for three color palettes; space, sunset, and dark rainbow. By simply changing the background color (combined with the color blending mode already set by the color palette) you can get some truly different and interesting results

Sparkle
There are 142 Rotae (27%) that have the sparkle feature, which drawns tiny circles within (and sometimes around) the line for some extra magic. This is usually only really visible when you see the image on a big screen though. Certain color palettes will always have a sparkle, such as snowflake and fog.

Background
I’ve loved spirographs since I was a kid. I had one of those kits and would draw all kinds of flower-y shapes. I would definitely get frustrated though when I made a tiny mistake with my pen, or the circle would move just a little. I could start all over again…

When I discovered programming years later, and especially when I dove into SVGs and d3.js, it didn’t take long before I found my way back to spirographs. Using code to create a spirograph will make it absolutely perfect, every time. It’s drawn near instantaneous, but you could also animate it. And, if you wanted, you could break the perfectness and sometimes get some very interesting results when the conditions were just right.
Officially “circles on circles” would be a fourier transform, epicycles would perhaps fit better, but I feel these shapes feel closer to spirographs. According to Piter Pasma these are “Polyepihyperderpflardioids”, which is an awesome name!
Best of all, you could work with an endless number of ‘wheels’, not being limited to the two that are possible in the physical realm, creating ever more intricate patterns. More than two wheels are no longer spirographs though. In fact Spirograph is only the name of the toy, not a mathematical description. However, most people know the term “spirograph” and what it conveys, so I’m often using the term “spirograph” to describe my results from this algorithm.
The purchase in March 2020 wasn’t a coincidence of course, having suddenly had all my clients and a vacation fall away.
I created an online page to randomly draw spirographs during 2016. However, it was through the pen plotter that I bought in March 2020 that I really got back into working with them. I started with bigger spirographs that would be as wide as an A4 page, going around hundreds of times before closing (if at all).

Wanting to learn more about the math underlying the idea of circles rotating on circles and their symmetry I came across the paper by Frank A. Farris about “Wheels on Wheels on Wheels”. I adjusted some of the math from there into my own code and started experimenting with 3 and 4 wheels, drawing a grid full of tiny tiny shapes.
I was amazed by the enormous variety of shapes that I saw and definitely wanted to dive even deeper. However, life went on and you get distracted by other things, work, etc… so I didn’t really touch it again for about a year.

When I started learning about NFTs during July of 2021 I quickly found the existence of Art Blocks and thought it would be damn amazing to be able to release a project for Art Blocks, having the code itself live on the blockchain. Since my expertise lies in the visualization of data, which wasn’t an option to use with Art Blocks, it was clear as day for me what I wanted my project to be based on instead; wheels rotating on wheels.
At first I tried to mimic the feeling/design of a pen plotter, but then made digitally. However, after some advice I pivoted away and instead focused on how I could draw these shapes in ways that would be near impossible with a pen plotter, really embracing the possibilities of the digital medium; gradients, backgrounds, vibrant poppy colors, changes in line thickness, different kinds of lines, etc.
During July and August I started with the code that I’d already made for my miniature pen plotted spirographs and took it several steps further to eventually become “Rotae”.
Charity
Of the proceeds of Rotae that were above the resting price 25% have been donated to two charities that I’ve long been following; $2229 to each charity.
The first charity I choose is The Ocean Cleanup, founded in the Netherlands that is dedicated to cleaning up our Oceans. The second is the Cheetah Conservation Fund. The Cheetah has been my favorite animal for as long as I can remember (ノ◕ヮ◕)ノ*:・゚✧ . I’m really happy to have supported both of these wonderful charities with Rotae!